created 2025-04-07, & modified, =this.modified
rel: When We Cease To Understand the World by Labatut
Why I’m reading
Frequently recommended book, that has been on my backlog for years.
My reason for delaying a read, is that it seems involved, and long but also a subject matter that I would enjoy, so I want to make sure that I am ready.
I’m also changed.
I’m not sure if I even like computers even more, the same way.
There are two kinds of creation myths: those where life arises out of the mud, and those where life falls from the sky. In this creation myth, computers arose from the mud, and code fell from the sky.
Von Neumann’s project was the physical realization of Alan Turing’s Universal Machine, a theoretical construct created in 1936. It was the first computer to make full use of a high-speed random-access storage matrix and was the first machine whose coding was the most widely replicated and whose logical architecture was the most widely reproduced.
Computers were essential to the initiation of nuclear explosions and to understanding what happened next. It is no coincidence that the most destructive and the most constructive human inventions appeared at the same time.
In answering the Entscheidungsproblem, Turing proved that there is no systematic way to tell, by looking at a code, what that code will do.
1953
Bit was coined by statistician John W. Tukey shortly after he joined von Neumann’s project.
That all communication can be written withtwo symbols was established by Francis Bacon in 1623.
The transposition of two Letters by five placeings will be sufficient for 32 Differences [and] by this Art a way is opened, whereby a man may expresse and signifie the intentions of his minde, at any distance of place, by objects … capable of a twofold difference onely
MANIAC (Mathematical and Numerical Integrator and Computer)’s first test was a thermonuclear calculation that ran for 60 days nonstop.
1953 - three technological revolutions
- thermonuclear weapons
- stored program computers
- elucidation of how life stores instructions on strings of DNA Regarding Watson and Crick - “If only specific pairs of bases can be formed, it follows that if the sequence of bases on one chain is given, then the sequence on the other chain is automatically determined.” Palindromic
Olden Farm
Lenape, and Lenni Lenape subset identified with the Turtle clan.
William Penn petitioned the king in 1680 for a settlement. The colony of Pennsylvania, with capital Philadelphia was the result. Penn traveled extensively into the surrounding wilderness learning Lenni Lenape language well enough to speak without an interpreter. He wrote of them, “The low dispensation of the poor Indian out shines the lives of those Christians, that pretend an higher.”
A worn Lenni Lenape foothpath became a trail passable by horses and wagon, “King’s highway” and finally route 27 and 206.
Thought
General Mercer, surrounded, refused to surrender and, mistaken for General Washington, was bayoneted and left for dead.
How you could, in the absence of actually seeing someone before, be mistaken.
Veblen’s Circle
Since Archimedes military commanders brought in mathematicians for help. With the advent of breech-loading, rifled artillery, accuracy improved to where it became possible to test-fire a gun a fixed number of times, and then use a mathematical model to complete a range table.
Veblen organized the teams of human computers who were placed under his command, introducing mimeographed computing sheets that formalized the execution of step-by-step algorithms for processing the results of the firing range tests.
NOTE
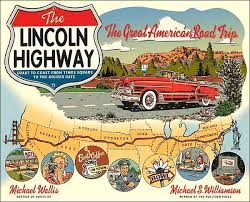
Lincoln Highway
In 1913 the Lenape footpath became part of the first transcontinental motorway across the US, the Lincoln Highway – beginning at Times Square and ending in the overlook above Point Lobos in San Fran.
The roadway itself was conceived by businessmen involved with the emerging, tire, gas and pavement industries. The federal government was not building roads, so their plan was to connect existing state roadways as “the Main Street across America.”
Institute for Advanced Study
Abraham Flexner envisioned, “a paradise for scholars who, like poets and musicians, have won the right to do as they please”
The institute was to be “the simplest and least formal thing imaginable” Each school would have a permanent group of professors and changing members, and they’d manage their own affairs and energy as pleasing to themselves.
Knowledge, not profit:
As a matter of history the scientific discoveries that have ultimately inured to the benefit of society either financially or socially have been made by men like Faraday and Clerk Maxwell who never gave a thought to the possible financial profit of their work.
“the pursuit of these useless satisfactions proves unexpectedly the source from which undreamed-of utility is derived.”
Out of practicality math was chosen as the initial focus (stimulating to scientists and poets alike, and without equipment needs – a few rooms, books, chalkboards and papers).
Oswald Veblen was appointed first professor, followed by Einstein, von Neumann, Weyl, James Alexander, and Marston Morse.
Established during the rise of fascism in Europe, the institute played a key role in the transfer of intellectual capital from Europe to America.
Veblen: “There is no educational institution in the United States which has not in the beginning made the mistake of acquiring too little rather than too much land.”
Princeton University professors referred to “the Institute for Advanced Salaries,” while Princeton University graduate students referred to “the Institute for Advanced Lunch.”
Aydelotte took over for Flexner, and was later succeeded by Oppenheimer in 1947.
Neumann János
Game Theory for Economists:
Under threats of cancelation by Princeton University Press over the manuscript’s escalating length, Theory of Games and Economic Behavior was finally published in 1944.
It was 673 pages in which Morgenstern and von Neumann make a case of how a reliable economy can be constructed out of unreliable parts,
“Unifications of fields which were formerly divided and far apart,” they counseled in their introduction, “are rare and happen only after each field has been thoroughly explored.”
von Neumann was drawn to impossible problems. He rarely appeared without a suit and a tie, a habit he attributed to being mistaken as a student when he began to teach at Princeton at age 26.
Axiomatization is the reduction of a subject to a minimal set of initial assumptions, sufficient to develop the subject fully without new assumptions having been introduced along the way. von Neumann started fresh at axiomatization of sets, where Russel And Whitehead had attempted (at 1,984 pages) with fundamental questions unresolved.
Gödel proved that within any formal system sufficiently powerful to include ordinary arithmetic, there will always be undecidable statements that cannot be proved true, yet cannot be proved false. Turing proved that within any formal (or mechanical) system, not only are there functions that can be given a finite description yet cannot be computed by any finite machine in a finite amount of time, but there is no definite method to distinguish computable from noncomputable functions in advance.
He, more than anyone I know,” adds Klári, “took it as a most personal affront that any nation, group of people, or individuals, could possibly prefer the base and unsophisticated philosophy of Nazism or any other ‘ism’ to such minds as Einstein, Hermann Weyl, Wolfgang Pauli, Schrödinger and many, many others including, last but not least, himself.”
Veblen devoted all available resources to rescuing as many mathematicians as he could.
“His hatred, his loathing for the Nazis was essentially boundless,” Klári adds. “They came and destroyed the world of this perfect intellectual setting. In quick order they dispersed the concentration of minds and substituted concentration camps where many of those who were not quick enough … perished in the most horrible ways.” Von Neumann bore the traces of this for life. “There was a surface there of a very convivial sort,” his daughter, Marina, explains, “which overlay what was fundamentally a rather cynical and pessimistic view of the world.”
von Neumann liked fast cars, which he bought yearly. He drove like mad and needed to sleep for only three or four hours a night.
He’d be able to write freely and fast on a subject that was “mature” in his mind, but succumbed to pedantism and inefficiency when writing on a subject he can believe is in its final form.
His handwritten letters sometimes end with an informal “P.S.” that continues, for several pages, to explain some new result.
In July of 1943 he was enlisted for “Project Y,” as the Manhattan Project was code-named.
“In March or April 1944,” says Metropolis, “von Neumann spent two weeks working in the punched- card-machine operation, pushing cards through the various machines, learning how to wire plugboards and design card layouts, and becoming thoroughly familiar with the machine operations.”
von Neumann acted “as if he knew there was not very much time left.”
As he came more and more to realize that the control over the physical forces of nature which he and his co-workers had placed in the hands of their fellow men could be used for evil as well as for good, he felt with steadily increasing intensity the moral problems bound up with the greatest of modern scientific triumphs.
MANIAC
Let the whole outside world consist of a long paper tape. —John von Neumann, 1948
ENIAC (electronic numerical integrator and computer) was the first computer to have all of these qualities: programmable, electronic, general-purpose and digital.

The electromechanical differential analyzer at the > Ballistic Research Laboratory (a ten-integrator version of the analog computer that Vannevar Bush had developed at MIT) took 10 or 20 minutes. To complete a single firing table still required about a month of uninterrupted work.
The ENIAC machine was designed to prepare a firing table in a few days.
 Programming was locally distributed among the individual processors, coordinated by a “master programmer” with a storage capacity of 60 bits.
Programming was locally distributed among the individual processors, coordinated by a “master programmer” with a storage capacity of 60 bits.
The ENIAC had 17,468 vacuum tubes and occupied a 33-by-55 foot room.
“The ENIAC itself, strangely, was a very personal computer,” remembers mathematician Harry Reed, who arrived at Aberdeen in 1950. “Now we think of a personal computer as one which you carry around with you. The ENIAC was actually one that you kind of lived inside.”
The ENIAC had the computational architecture of a roomful of twenty human computers working with ten-place desk calculators and passing results back and forth.
The ENIAC was programmed by setting banks of 10-position switches and connecting thousands of cables by hand. Hours, sometimes days, were required to execute a programming change.
Data and instructions were intermingled in the machine. Some pulses were used to control operations, some to signify data.
Storage was the main limitation. A comparison is made of locking people up in a room for 3 years, giving them desk multipliers and they cannot write more than a full page. They can erase any amount to put it back again, but it is clear where the bottleneck lies.
Punch cards were used to store intermediate results, but it was slow and error prone. A hydrogen bomb calculation consumed nearly one million cards and most of them were for temp storage of intermediate results. In a sense though, this made the storage infinite.
The functions of the von Neumann architecture of computer were
- a hierarchical memory,
- a control organ
- a central arithmetic unit
- and i/o channels
Von Neumann knew that the real challenge would be not building the computer, but asking the right questions, in language intelligible to the machine.
Fuld 219
We have been trying to see how far it is possible to eliminate intuition, and leave only ingenuity. We do not mind how much ingenuity is required, and therefore assume it is to be available in unlimited supply. – Alan Turing 1939
Von Neumann believed that Hilbert’s goal of a final and conclusive axiomatization of math was limited. He wrote to Gödel after hearing hints of the incompleteness proof in his announcement, but Gödel beat him to it, to his disappointment.
Going against the prevalent:
“He was more than capable of this, had he admitted to himself the possibility that Hilbert was wrong in his program. But it would have meant going against the prevailing thinking of the time.”
The Gödels, holding German passports, were required to register as enemy aliens, and could not leave Princeton without written permission from the Department of Justice in Trenton, even for routine visits to their doctors in New York.
Proposed by George Cantor in 1877 the continuum hypothesis states that the set of real numbers (the continuum) is the smallest infinity whose size is larger than the set of integers and that not intermediate-sized infinities lie between. Gödel proved within a strictly defined system it was impossible to disprove the hypothesis. “Please send Gödel continuum hypothesis notes,” Alan Turing cabled from King’s College, Cambridge, on December 16.
Kurt then went on to be preoccupied with cosmology, as result of discovering a solution to Einstein’s equations that implied a rotating universe, and the legacy of Gottfried Wilhelm Leibniz, the 17th century pioneer of calculus, binary arithmetic and universal language – believing much of his work had been lost or concealed.
Critics dismissed Gödel’s study of the Leibniz manuscripts as a waste of his mathematical talents, verging on the occult, but according to von Neumann, “a man of his caliber and record ought to be the sole judge of what he does.”
Leibniz theorized was selected from an infinity of possible universes, optimized so that a minimum of laws would lead to a maximum diversity of results.
He saw binary coding as the key to a universal language and credited its invention to the Chinese, seeing in the hexagrams of the I Ching the remnants of “a Binary Arithmetic.”
Leibniz’s belief in a universal digital coding embodied his principle of maximum diversity: infinite complexity from finite rules. “Nothing is a better analogy to, or even demonstration of such creation than the origin of numbers as here represented, using only unity and zero or nothing”
6J6
The fundamental, indivisible unit of information is the bit. The fundamental, indivisible unit of digital computation is the transformation of a bit between its two possible forms of existence: as structure (memory) or as sequence (code). This is what a Turing Machine does when reading a mark (or the absence of a mark) on a square of tape, changing its state of mind accordingly, and making (or erasing) a mark somewhere else.
A binary counter is simply a pair of bistable cells communicating by gates having the connectivity of a Möbius strip
John von Neumann:
The part that is stable we are going to predict. And the part that is unstable we are going to control.
Weather modeling
While trying to simulate weather inside the computer, the meteorologists were plagued by the weather outside the computer. The “York” refrigeration units continued to become overloaded in the sultry Princeton heat, and during thunderstorms the Williams tube memory often failed. On one very hot day in May there was trouble with the IBM card equipment, and the machine log records: “IBM machine putting a tar-like substance on cards.” The next log entry explains: “Tar is tar from roof.”
Barricelli was a pioneer in artificial life research. He programmed the first genetic algorithm.
Barricelli punch cards:
Barricelli “insisted on using punched cards, even when everybody had computer screens,” according to Gaure. “He gave two reasons for this: when you sit in front of a screen your ability to think clearly declines because you’re distracted by irrelevancies, and when you store your data on magnetic media you can’t be sure they’re there permanently, you actually don’t know where they are at all.”
On error, and digital organisms:
For complementary reasons, digital organisms—whether strings of nucleotides or strings of binary code—may find it advantageous to translate themselves, periodically, into analog, nondigital form, so that tolerance for ambiguity, the introduction of nonfatal errors, and the ability to gather tangible resources can replenish their existence in the purely digital domain. If “every error has to be caught, explained, and corrected, a system of the complexity of the living organism would not run for a millisecond,” von Neumann explained in his fourth lecture at the University of Illinois. “This is a completely different philosophy from the philosophy which proclaims that the end of the world is at hand as soon as the first error has occurred.”
Barricelli evolved numerical organisms that learned to play a simple but non-trivial game on a 6x6 board called Tac-Tix. Game performance was linked to reproductive success.
 Barricelli:
Barricelli:
“If humans, instead of transmitting to each other reprints and complicated explanations, developed the habit of transmitting computer programs allowing a computer-directed factory to construct the machine needed for a particular purpose, that would be the closest analogue to the communication methods among cells.”
Turing’s Cathedral
“One of the facets of extreme originality is not to regard as obvious the things that lesser minds call obvious,” says I. J. (Jack) Good
Turing’s machine (which he termed an LCM, or Logical Computing Machine) thus consisted of a black box (as simple as a typewriter or as complicated as a human being) able to read and write a finite alphabet of symbols to and from a finite but unbounded length of paper tape—and capable of changing its own “m-configuration,” or “state of mind.”
In the halting function, Turing called configurations that halt “circular” and configurations that keep going indefinitely “circle free” and demonstrated that that unsolvability of the halting problem implies the unsolvability of a broader class of problems including the Entscheidungsproblem (decision problem).
Turing showed that undecidable statements, resistant to the assistance of an external oracle, could still be constructed, and the Entscheidungsproblem would remain unsolved.
What if intuition could be replaced by ingenuity, and ingenuity, in turn, by brute force search? “We are always able to obtain from the rules of a formal logic a method of enumerating the propositions proved by its means. We then imagine that all proofs take the form of a search through this enumeration for the theorem for which a proof is desired. In this way ingenuity is replaced by patience.”
In the real world most of the the time finding an answer is easier than defining the question. It is easier to draw something that looks like a cat than to define what, exactly, makes something look like a cat. “An answer finds a question, not the other way around.”
“I agree with you about ‘thinking in analogies,’ but I do not think of the brain as ‘searching for analogies’ so much as having analogies forced upon it by its own limitations,” Turing wrote.
Thought
In On Lying in the Bed and other Essays by G.K. Chesterton Chesterton talks about how ever horse a man draws will be partly human. I think this is because it is because it is part of the man’s vision. We really just see the insides of our heads.
Random search can be more efficient than nonrandom search.
A random network, whether of neurons, computers, words, or ideas, contains solutions, waiting to be discovered, to problems that need not be explicitly defined. It is easier to find explicit answers than to ask explicit questions. This turns the job of the programmer upside down. “An argument in favor of building a machine with initial randomness is that, if it is large enough, it will contain every network that will ever be required,” advised Good, speaking to IBM in 1958
Instead of learning from one mind at a time, the search engine learns from the collective human mind, all at once. Every time a human searches something, and finds an answer, this leaves a faint lingering trace to where (and what) some fragment of meaning is. The fragments accumulate and, at a certain point, as Turing put it in 1948 – “the machine would have ‘grown up’”.
Self-Reproducing Automata
Over long distances it is expensive to transport structures, and inexpensive to transmit sequences. Turing machines, which by definition are structures that can be encoded as sequences, are already propagating themselves locally, at the speed of light. The notion that one particular computer resides in one particular location at one time is obsolete.
It’s easier to write a new code than to understand an old one - von Neumann